介绍 #
随着IP复用,业界一度试图使用IP内部资源进行布线,但此举可能引发噪声和转换电压过大,因此绕障策略在布线算法中发挥着重要的作用。
曼哈顿结构以及非曼哈顿结构 #
总体布线的布线算法主要基于曼哈顿结构以及非曼哈顿结构两种,非曼哈顿结构因其更强的布线优化能力受到越来越多研究人员的关注。布线互连结构可分为曼哈顿结构和非曼哈顿结构。曼哈顿结构的布线方向只能是水平走线和垂直走线两种,而非曼哈顿结构的布线方向则更为多样化,主要包括走线方向为 **0°、90°和士45°**的X结构以及走线方向为 0°、60°和 120°的Y结构。随着系统级芯片(System-on-a-Chip,SoC)设计概念的出现和制造工艺的不断发展,**互连线的延迟对 VLSI设计的影响越来越大,同时互连线的不断增长会降低芯片的速度,造成过高的功耗以及增大噪声,**这要求更有效的互连线线长优化和更强的电路性能。但基于曼哈顿结构的相关物理设计阶段在优化互连线线长时限制了相关策略的优化能力。为优化芯片的整体性能,相关研究人员开始尝试基于非曼哈顿结构的布线。
非曼哈顿结构的数学基础是λ-几何学理论
(1)当λ=2时,布线的方向为ix/2,走线方向包括 0°和 90°,对应传统的曼哈顿结构,亦称为直角结构。 (2)当λ=3时,布线的方向为 iπ/3,走线方向包括 0°、60°和120°,称为Y结构。 (3)当λ=4时,布线的方向为 i/4,走线方向包括0°、90°和士45°,称为X结构。已经得到工艺支持
意义 #
物理设计过程是EDA的主要处理对象,是人工最易出错的
当前,超大规模集成电路(Very Large Scale Integration Circuit,VLSI)设计在许多高科技电子电路的发展中起着至关重要的作用。当前集成电路(IntegratedCircuit,IC)产业向超深亚微米工艺不断推进,芯片的集成度进一步提高,一块芯片上所能集成的电路元件越来越多,VLSI是将数百万个品体管集成到单个芯片中形成 IC 的过程。这一市场趋势对**物理设计(Physical Design,PD)和物理验证(Physical Verification,PV)**提出了许多挑战。以 VLSI为基础的电子信息产业的发展,对我国国民经济的发展、产业技术创新能力的提高以及现代国防建设都具有极其重要的意义。
物理设计是VLSI构建流程中最为耗时的,其设计好坏将影响芯片的最终性能,包括时延特性,电能消耗、电路稳定性等。
近年来 ,集成电路领域发展越来越迅猛 ,晶体管数量随集成电路制造⼯艺发展逐年增加 ,芯片内包含的逻辑门数量急剧提升 ,这给集成电路设计带来了巨大的难题。由于超大规模集成电路(very-largescale integration circuit,VLSI)逻辑的高度复杂性 ,其物理设计往往需要使用计算机辅助设计⼯具来完成。这就向电子设计自动化(electronic design automation,EDA)⼯具提出了严峻挑战
在物理设计过程中 ,布线是极其重要的一环 。布线⼯作占据了 EDA 过程的大部分时间 ,甚至在大部分情况下 ,自动布线的结果还需要设计人员在后期手⼯调整。具备优秀的布线速度及高布线质量的布线器对缩短芯片设计周期有着至关重要的作用 。
布线 #
在物理设计中需要采用电路划分方法将复杂庞大的电路系统分解至合理小的电路子系统;其次,在电路划分后,布图规划和布局步骤则是将不同形状和大小的单元或模块合理地放置到芯片的不同布线区域,同时满足芯片固有的一些相关几何约束;再次,布局阶段确定模块和引脚各自的位置,在此基础上经总体布线后,将每条待绕线的线网的各部分合理分配到芯片中的各个布线通道区;最后,由详细布线得到各个布线通道区的实际绕线。
模型输入输出 #
输入 #
- cell, pin’s position
- netlist graph(connection relation)
- 设计工艺:多少层,via几何形状信息,各种drc
- 部分关键线网延时信息
- wire和via的电气特性
输出 #
一个尽可能满足约束条件并更少得需要人⼯调整线网的布线结果
网表内各线网的连接⽅式 ,包含金属线及通孔的几何描述信息
约束 #
- 线网连接正确性
- 布线障碍 :指布线过程中被占用的区域,包括逻辑单元及芯片版图中的布线障碍 ,以及部分已布线网 ,如电源线网和时钟线网等
- 版图设计规则 :主要由制造⼯艺决定。制造厂商在制造过程中 ,为满足芯片最基本的可制造性 ,尽可能让芯片的设计可用 ,根据现有的制造技术设计了种种版图设计规则。设计规则违反(design rule checking violations,DRC)的数目很大程度上代表了布线质量的高低。 主要包含:
- 金属线的最小宽度(min-width);
- 金属线间及金属线与布线障碍间的最小线间距(min-spacing);
- 一条金属线的最小面积(min-area),当金属线的宽度固定为最小宽度时 ,最小面积约束也被称作最小长度约束
总体布线 #
又称概略布线,全局布线

总体布线负责合理将每条线网的各部分分配到各个布线通道区中(也就是分配布线资源)并明确定义各布线问题
总体布线的结果对详细布线的成功与否起到决定性作用,同时总体布线严重影响最后制造出来的芯片性能。
一个经典图论问题
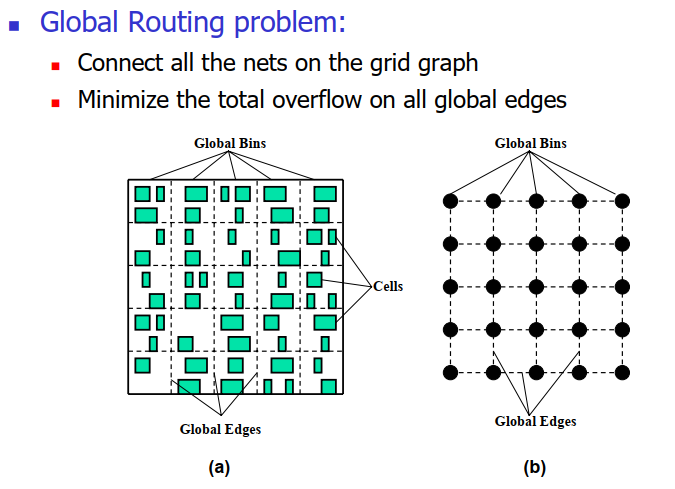
整个芯片被分为多个区域 ,并将线网的连接关系对应到区域上 ,在区域间连线。由于全局布线不需要考虑版图设计 规则的约束 ,甚至不需要考虑大部分几何级问题 ,其布线模型的建模较为简单 ,即使在具有数以万计的区域的芯片版图上布线,也只产生较低的时间开销
总体布线中首先将可布线区域划分成多个小格,每个格的布线资源使用带容量的边来表示,所有布线资源由一个网格图表示;再确定一个线网所占用网格图中的边,即线网的大致走线,将各线网合理地分配到各个网格中,以确保尽可能高的布通率。
**总体布线图(Global Routing Graph, GRG)**将布线区域、每个区域内的布线容量、布线区域内的引脚信息以及不同布线区域之间的相互关系等信息抽象为一张图。不同的设计模式产生多种布线图模型,常见的布线图模型主要包括网格图模型、布线规划图模型以及通道相交图模型
即使是最简单的问题,如一组两引脚线网在拥塞约束下布线,也是一个NP 完全问题。
全局布线的主要目标是为后续的详细布线提供指导 ,从而降低布线问题的复杂程度 ,减少整体的时间开销。作为整个布线任务中多种优化目标的主要影响因素 ,全局布线要在给定布线资源的情况下 ,优化线长、通孔数及关键线网时延等目标函数
评价全局布线算法的主要指标有线长、通孔数、溢出数 量、运行时间
布线图模型 #
网格图模型 #

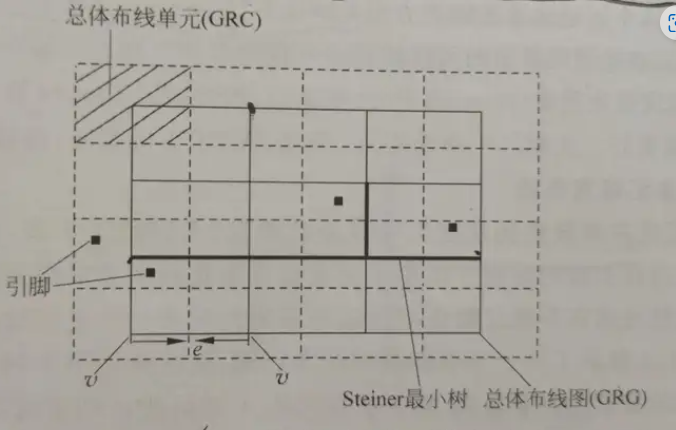
一个顶点表示一个总体布线单元(Global Routing Cell,GRC),GRC之间的连接关系则由水平边和垂直边表示。
对于给定的线网集合,则将它们的引脚集合按照其所在的总体布线单元,映射到该总体布线单元对应的顶点上
每一个全局布线单元(GRC)被视作全局布线问题中的一个点 ,相邻近的单元所代表的点之间具备一条有容量的边 ,对应相邻单元间的边界 ,这条边的容量代表能穿过此边界的金属线的最大数目 。因此 ,可以通过各边的容量与穿过边的金属线数量估计全局布线的资源拥挤程度。
布图规划图模型 #
通道相交图模型 #
算法 #
最早用于解决总体布线图上的最短路径问题的是1959年出现的Diikstra算法,该算法的时间复杂度为 O(n^2^)
后来发展为迷宫系列算法,缺乏寻找最优解的能力,不适用VLSI
多引脚网分解 #
多引脚线网分解常用于总体布线算法。具有两个以上引脚的线网通常被分解成两个引脚的子网,然后每个子网的点对点布线以某种串行方式执行。这种线网分解是在总体布线开始时执行的,这会影响最终布线结果的质量。许多总体布线都采用多引脚线网分解。分解多引脚线网的两种流行方法是RSMT构造和最小生成树(Minimum Spanning Tree,MST)构造。RSMT 通常提供较短线长的树状拓扑结构,而 MST 由于产生更多的工形双引脚线网而提供更大的灵活性。
最小树算法 #
Steiner 最小树算法 #
多端点线网的总体布线可定义成寻找 Steiner 树问题,精确算法、传统启发式算法、计算智能方法都可用于求解 Steiner 树。
在VLSI总体布线问题中,多端线网的总体布线问题是寻找一棵连接给定引脚集合的布线树问题,而 Steiner 最小树相对于其他方法所得的布线树来说具有更小的布线树总线长。因此,Steiner最小树被看作总体布线问题中多端线网的最佳连接模型,并且在总体布线图上的Steiner 最小树算法是所有总体布线算法的基础。
精确算法包括动态规划技术、拉格朗日松弛法、分支界限法等。虽然从理论上能够得到问题的精确解,但是问题规模越大,精确算法越难求解问题。继而研究工作开始转向启发式策略。遗传算法、蚁群算法、鱼群算法、粒子群优化算法等计算智能方法在求解 Steiner 问题中展示出了广阔的应用前景。
近年来,随着计算能力的增强,加之高性能电路的设计需要,版图设计技术也将随之改进。出于增强电路的性能的目的,研究人员提出新型互连结构,即非曼哈顿互连结构,非曼哈顿结构 Steiner 树则应运而生。
然而,精确算法受其复杂度限制不适用于求解非曼哈顿结构 Steiner 树这类NP难问题,而贪心策略致使传统启发式算法极易过早收敛。据所查找的资料文献中,目前将计算智能方法应用到求解该NP难问题的研究工作还较少。
整数线性规划布线 #
慢
拆线重步 #
在确定了一组线网的初始布线后,通常会发现一些布线资源被过度使用了。然后,现有的布线被拆开,重新分配到一个迭代修复框架中,这个框架被称为“拆线重布”。现代整数线性规划工具帮助基于整数线性规划的总体布线在数小时内成功完成数十万条布线。然而**,商业EDA 工具需要更大的可扩展性和更少的运行时间**。在布线阶段,如果一个线网无法布线,通常是由于物理障碍或其他布线线网占用了它的路径。核心思想是允许临时违规,直到所有线网都被布线。也就是说,迭代地拆开一些线网,并以不同的方式重新对它们布线,以减少违规的数量。如果一次只处理一个网,那么这个策略就是串行法,所以线网的串行处理对最终解的质量影响很大。 文献[31]对于每一个违规的线网定义了拆线重布的成功率,并且只对最有希望改进的线网重布线。然而**,若一个线网在没有违规的情况下不能布线,那么成功率需要重新计算。这是非常昂贵的,尤其是对于大规模的设计。**拆线重布通常与其他总体布线方法相结合,作为进一步提高布线质量的后处理步骤。
协商拥塞布线 #


层分配问题 #
层分配在可布线性、时序性、串扰性和可制造性方面起着至关重要的作用。如果特定层分配的导线数量过多,则会加剧拥塞和串扰。此外,如果总体时序关键线网被分配到较低层,则时序由于导线宽度/间距较窄而恶化。差的层分配产生的大量通孔,其比线需要更大的面积和更宽的间距,进而导致可布线性/引脚访问问题。对于纳米设计,最小化通孔数量尤为重要,因为通孔故障是关键的可制造性问题之一。层分配是多层总体布线中的关键步骤,因为它将二维总体布线的结果映射到原始的多层解空间。现代集成电路或芯片通常是多层结构。在布线时,大多数布线器通常不会在三维空间中直接布线。相反,它们在二维平面上布线,然后通过层分配技术将二维布线结果恢复到三维空间。有些工作是基于动态规划实现的,此外,BoxRouter 2.0实现了一种复杂的线性规划技术,可以根据二维投影恢复三维布线,并根据三维布线结果优化二维布线器。**层分配的目标通常是保持二维总体布线的总溢出,然后最小化通孔数量。**在层分配中考虑天线效应,通过适当地将导线分配到较高的金属层(不一定是顶层),可以有效地减少天线违规

一个k层的布线区域可以被划分为一大批的总体布线块并建模成为k层网格图G^k^(V^k^,E^k^)。其中k表示布线层的数量,V ^k^表示第k层网格总体布线单元的集合,E^k^表示第k层的网格布线边,其中每条边表示相邻布线块的边界。相邻层的连接边表示通孔。一条网格边的容量定义为可以经过相邻布线块的布线轨道数。
层分配定义:

串行和并行方法 #
串行 #
布线多个线网的最原始和最简单的策略是选择特定的顺序,然后按该顺序布线线网。这种方法的主要优点是:在布线当前线网时,可以知道并考虑前期布线线网的拥塞信息。例如,在将多引脚线网分解成两引脚线网的早期算法中,使用绕障迷宫布线或线路探测布线等方法来对每个线网布线。在这些方法中,单元边界对路径搜索开放,直到所有的路径都被先前考虑的线网占据。在这一点之后,边界被视为障碍。顺序法的缺点是解的质量很大程度上取决于线网的处理顺序,很难找到好的顺序。在任意特定的顺序下,由于过多拥塞,很难对后期的线网布线。
此外,没有反馈机制允许这些线网将信息反馈给前期布线的线网,以便为后期布线的线网留下一些区域。文献[109]提到没有一种单一的线网排序方法始终表现良好。尽管对于线网的排序问题上存在争议,但在串行布线上已经有了一些很好的研究成果,主要是通过迭代循环将后期布线的线网的拥塞信息反馈给前期布线线网
虽然串行方法、拆线重布以及其他启发式方法在实践中可能是有效的,但是它们不能提供关于是否存在可行解决方案的具体答案。换句话说,如果这些方法不能找到可行的解决方案,不清楚这是因为可行的解决方案不存在,还是因为启发式方法的缺点。另外,当启发式方法找到可行解时,不知道解是否最优,与最优解相差多远。?
依据预先给定的线网顺序对线网进行布线,布线过程中先布线网会抢占后布线网的布线资源,不同的布线顺序可能会生成完全不同的布线结果。早期的一项研究指出,在布线开始之前找到一个最优布线顺序是NP难问题,且不存在一个在所有情况下都达到最优的布线顺序选取策略叨。对所有线网同时进行布线的同时布线算法可以避免线序对布线结果的影响。
策略:
- 按端点数量的升序布线。端点数量较多的线网往往会造成内部空间的拥塞。
- 按线长升序布线以降低容量溢出 ,提升可布性。线长较短的线网布线范围比较小 ,灵活性有限 ,而线长较长的线网则可以在更大范围内绕路 ,寻找更优解。
- 按线长降序布线以降低总体时延。优先布线长较长的线网 ,降低线长较长 的关键线网对总体时延的影响 ,以提升电路的总体性能。
- 依据预估的拥塞程度布线 ,优先对较为拥塞的区域内的线网进行布线
并行 #
在串行方法中,路径是根据预定的顺序一次生成的。串行方法是非常快速的,但由于它们的串行性质会导致次优解。并发方法试图利用总体优化方法来解决问题。这些方法可以提供电路布线的总体视图,但需要相当长的时间。从计算复杂性的角度来看,所有网络的并发布线是一个**复杂的问题。使用整数线性规划是实现这一目标的方法之一。**事实上,总体布线问题的数学模型可以修改为 0-1整数规划问题。线性规划由一组约束和可选目标函数组成。这个函数根据约束判断是最大还是最小。约束和目标函数都必须是线性的。这些约束形成了一个线性方程和线性不等式的系统。整数线性规划是一种特殊的线性规划,其中每个变量只能取整数值且都是二进制的,故称为0-1整数线性规划。

基于并发方法的总体布线器包括对布线区域拥塞的评估,产生了高质量的布线。另外,舍弃可能处于拥堵区域的路径,以减小整数线性规划的输入规模。
多商品流(multi-commodity flow,MCF)算法将布线问题看作是一个多商品流问题回,并将其建模成整数线性规划(integerlinear programming,ILP)问题进行求解。
两端线网与多端线网 #
两端线网 #
迷宫布线算法 #
及其变体 A*算法:一般通过设计开销函数来躲避拥塞。开销函数的值往往在边界上穿过的金属线数量接近及超过边容量时迅速增大[9],迷宫布线类算法具备着极其强大的拥塞避免能力 ,可以对单个线网给出质量极高的布线结果 ,但即使通过开销函数定向减小搜索空间 ,迷宫布线类算法仍然会产生较高的时间开销
模式布线 #
使用预先设计的模式对两端线网进行布线 ,常用的模式有 L 型(1 拐点)、Z 型(2拐点)[10]与 U 型(2 拐点 ,绕路连线)
 由
于路径的搜索空间远小于迷宫布线 ,模式布线类算
法具备极快的布线速度 ,但其布线结果相对较差 。对于跨越 m × n 网格的两端线网 ,L 型模式仅在两种布线⽅式中选取代价较低的一种 ,而 Z 型模式会考虑 m + n 种不同的布线⽅式。因此 ,Z/U 型模式避免拥塞的灵活性要远大于 L 型算法 ,但相应地 ,其单个线网的布线时间复杂度更高
由
于路径的搜索空间远小于迷宫布线 ,模式布线类算
法具备极快的布线速度 ,但其布线结果相对较差 。对于跨越 m × n 网格的两端线网 ,L 型模式仅在两种布线⽅式中选取代价较低的一种 ,而 Z 型模式会考虑 m + n 种不同的布线⽅式。因此 ,Z/U 型模式避免拥塞的灵活性要远大于 L 型算法 ,但相应地 ,其单个线网的布线时间复杂度更高

单调布线 #

随布线问题复杂度的上升 ,L/Z/U 型模式布线已经不能满足问题的需求 。,其布线路径单调地向右上 ( 左 下 )或 左 上( 右 下 )搜 索 ,可 以 搜 索 到 (m + n - 2)!/ (m - 1)!(n - 1)! 种布线⽅式 ,且时间复 杂度与 Z 型相同 ,为 O (mn),但由于其走线拐点较 多,其布线通孔数会增加。
三拐点布线(3-bend routing), #
其路径支持最多 3 个拐点 ,且可以绕路布线。三拐点布线同样使用 O (mn)的时间复杂度 ,具备与迷宫布线相近的拥塞避免能力 ,且由于其最多使用 3 个拐点,极大地减少了通孔数
多端线网 #
很难直接使用迷宫布线或模式布线进行求解,主流的解决⽅法是最小斯坦纳树
steiner最小树算法 #
给定平面上的点Steiner 最小树通过一些 Steiner 点将这些点连接起来,以获得最小的总长度。
Steiner 最小树(Steiner Minimum Tree,SMT)作为超大规模集成电路物理设计的基本模型之一,可以应用于布图规划、布局和布线阶段。
作为一个标准的计算机问题,业界一般将布线问题代为Steiner最小树问题
Steiner最小树问题是一个NP难问题
Steiner 最小树通常用于物理设计中非关键线网的初始拓扑创建。最小化线长不是时序关键线网优化的唯一日标。然而,大多数线网在布线阶段是不重要的,Steiner 最小树给出了这种线网最理想的布线形式。因此,在布局规划和布局期间,Steiner 最小树通常被用来精确评估拥塞和线长。
对单个线网的布线,是物理设计中的一个基础问题。无论是总体布线还是详细布线,都会用到线网布线。线网布线又根据线网引脚的个数分为两引脚线网布线和多引脚线网布线。考虑到布线长度最小化,两引脚线网布线在布线图中就转换为最短路径问题,而多引脚线网布线转换为直角 Steiner 最小树(RectilinearSteiner Minimal Tree,RSMT)问题
拥塞图与拆线重布(rip-up and reroute) #
随着问题复杂度的上升 ,全局布线的布线资源越来越紧张 ,直接进行布线会发生大量无法避免的溢出
FastRoute[9]使用 FLUTE 算法生成的 RSMT 计算出拥塞图 ,并依据此拥塞图重新构建 RSMT
在拥塞图的初始化阶段 ,对所有两端线网分别进行拥塞程度计算。若两端点在水平或竖直⽅向具有相同的坐标 ,则直接将拥塞图上两端点间所有的边的拥塞程度加 1.0 。 否则 ,对于两⽅向上坐标都不相同的线网 ,计算其两种可能的 L 型连接⽅式 ,并将两种可能的路径上的边的拥塞程度都加 0.5
拥塞图的初始化阶段过后 ,由于所有 L 型连接⽅式都在拥塞程度上平均分配 ,在拥塞程度较大的区域 ,拥塞程度可能会超过其容量。为了更好地规划拥塞图的拥塞分布 ,使用一个快速的拆线重布 ,依次将各 L 型连接的两端线网提供的拥塞程度去除后 ,选择拥塞程度更小的一条路径 ,并将此路径的拥塞程度加 1.0。
拆线重布(rip-up and reroute)策略在初次布线完成后 ,对发生溢出的拥塞区域的线网进行拆除 ,并迭代地调整线序多次重新布线 ,直到溢出不再减少 ,或达到运行时间限制为止。
一般来讲 ,在初始布线时使用模式布线 ,这样在大量简单线网上拥有极快的布线速度 ,在拆线重布阶段 ,使用迷宫布线类算法 ,或时间复杂度较高的模式布线算法 ,以尽可能地提升重布线网的灵活性 ,并减少溢出次数 ,从而在整体的运行速度和布线质量间取得平衡
优化目标 #
主要是以减小通孔数量,还要考虑时延问题
随着器件尺寸迅速缩小,互连延迟对芯片性能产生了至关重要的作用。因此,最小化线路长度和延迟变得越来越重要。由于互连延迟已成为决定系统性能的主要因素,仅考虑拥塞已经不够。在布线过程中,加入时序约束和功耗约束更符合实际工业制造,无论是理论研究还是实际生产都具有重要意义。
主要研究方向 #
- 减少拥塞数和溢出数
- 考虑延时、串扰、拥塞等优化目标
- 非曼哈顿结构
- 并行
总体布线器 #
ISPD举行的 VLSI 总体布线算法竞赛中,涌现出了: [FGR]( https://web.eecs.umich.edu/~imarkov/pubs/conf/iccad07-fgr.pdf#:~:text=routing technologies and outperform the best), BoxRouter 2.0, [GRIP]( https://jlinderoth.github.io/papers/Wu-Davoodi-Linderoth-10-PP.pdf#:~:text=GRIP: Global Routing via Integer Programming), NCTU-GR2.0, [NTHU Route 2.0]( https://www.cs.nthu.edu.tw/~tcwang/nthuroute/#:~:text=NTHU-Route 2.0 is a fast and)
到目前(2022.05)为止,性能最好的几款布线器分别是NTHU-Route20、FastKoute 4.NCTU-GR 2.0和 MGR。NCTU-GR2.0在所有学术布线器中性能最好,它使用两种有界迷宫布线算法(最优有界迷宫布线和启发式有界迷宫布线),这两种算法的布线速度比传统的迷宫布线算法快得多。此外,串行总体布线算法,在多核平台上开发了并行多线程总体布线器。MGR是一款多级3D布线器,运行速度比传统3D布线器快得多。近两年来,研究者们尝试采用基于机器学习的方法解决总体布线问题。
时序驱动的总体布线器TIGER
FastRoute 1.0 #
串行
使用steiner结构避免迷宫路径
实现过程 #

#
FastRoute 2.0 #
串行

#

FastRoute 3.0 #
串行


详细布线 #
每个通道区中的最终布线将由详细布线来实现
详细布线是在尽量遵守总体布线的结果导向的前提下寻找每个布线片段的具体轨道位置,并绕开拥挤区域,同时尽可能满足一些基础的布线设计规则
在全局布线完成后 ,整个芯片的布线区域中较粗粒度的连接⽅式已经初步确定 ,但全局布线中GCell 之间的连接还不能直接表示成金属线 ,需要对GCell 之间的连接进行轨道分配 ,也是详细布线的前置步骤之一。此后 ,详细布线要在局部范围内满足线网连通率、设计规则违反等关键约束 ,并尽量降低线长和通孔数。
现代 VLSI 主流的布线策略为区域布线 ,布线过程中依据全局布线网格将整个芯片的布线区域分割成多个详细布线窗口(detail routing window),每个详细 布 线 窗 口 可 由 m × n 的 GCell 组 成( 一 般 取m = n),更大的详细布线窗口会导致更大的时间和内存开销,但可以改善布线的质量。
详细布线的布线图 ,即寻路算法的搜索空间,主要有两种构建⽅式:基于网格的(grid-based)和无网格的(gridless) 。
无网格布线允许金属线放置在布线区域的任意位置上 ,具备较高的布线灵活性。其在每个金属层上 ,使用树结构分割金属层上的几何形状[27],随后使用瓦片结构[28]或连接图[29]构建路径搜索算法的搜索空间。 由于无网格布线算法会产生较大的时间开销 ,大部分布线算法都使用布线网格构建搜索空间。
举例 #

算法 #
大多数是串行算法,为了弥补线网顺序对布线结果的影响,串行布线通常采用拆线重布的方式进一步精炼布线结果,可快速获得质量较好的布线方案
详细布线算法在给定布线网格中找到一个合法的布线路径
最短路径问题
李氏算法 #
老旧
A星算法 #
李氏算法的加速版本
GDRouter #
提出一个结合总体布线方法和详细布线方法的布线器,从而获得包含总体布线和详细布线的完整布线结果。
Algorithms and Data Structures forFast and Good VLSl Routing #
一个详细布线器,包含快速网络和形状网络结构两种数据结构
Detailed routing algorithms for advancedtechnology nodes #
最短路径算法未能寻找出合理的布线方案时,提出了一种多标签的最短路径算法,用于计算一些不违反设计规则的路径。
MCFRoute& A_Multicommodity_Flow-Based_Detailed_Router_With_Efficient_Acceleration_Techniques #
设计了一种基于多商品流模型的并行详细布线算法,同时对多个线网进行布线。但是这类算法并未考虑到时延优化问题且时间复杂度高。
轨道分配问题 #
是全局布线与详细布线的中间步骤
全局布线生成的布线结果仅仅完成了 GCell 级的连接 ,连接的路径被称为线段(segment)。在轨道分配阶段中 ,segment 特指没有几何形状及位置信息的线段 ,只表示 GCell 间的连接关系。而轨道分配算法中考虑其实际几何形状 ,更贴 近详细布线中金属线的线段被称作 iroute

在全局布线网格中 ,水平( 竖直 )⽅向的一行(列)GCell 共同构成一个面板(panel),其⽅向与对应布线层的优先走线⽅向一致,如图 4 所示。每个面板由多条布线**轨道(track)**构成 ,轨道的数量与全局布线边的容量相同。将所有线网的 iroute 都分配至轨道上 ,并保证一个面板内不同线网的各个 iroute 在同一轨道上没有重叠,是轨道分配⼯作的主要任务

到最优的轨道分配策略被证明是NP难问题
优化目标 #
最小重叠代价, 最小线长
举例 #

参考 #
Negotiation-based_track_assignment_considering_local_nets #

TraPL #

难点与挑战 #
十几年来,物理设计是集成电路中发展速度最快和自动化程度最高的领域之一。随着集成电路的特征尺寸不断减小,超大规模集成电路的工艺和电路规模以摩尔定律经历了巨大的进步,电路设计中不断增长的复杂性进一步扩大了物理设计中自动化设计问题的难度,并同时迎来一系列新的挑战。
在SRC发布的“Physical Design CAD Top10 Needs’”中指出的当前物理设计亟待解决的十大问题中,布线问题位居前列,在芯片尺寸和容量上,布线工作需要绕线的电路芯片规模达到成千上万个大模块和几百万个小模块,同时要求在合理可行的时间内完成布线工作。同时,VLSI物理设计中的其他一些需求,如定时和互连线分析,都对布线结果的质量有很高的要求。
在电路规模变大,尺度减小,复杂度飙升的今天,决定边权成为了一个十分重要的问题,随着待优化指标的增多,准确算法的时间空间复杂度均逐渐来到了一个不可接受的地步(毕经这是一个NP-Hard问题),因此业界主流的发展方向是使用近似算法。关于Steiner最小树的研究非常多,目前的理论最优解是 Geosteiner 算法
随着集成电路设计工艺的不断发展,允许绕线的布线层数随之增加,大幅度减少了互连线宽度和互连线间距,从而提高了集成电路的性能和密度。于是,多层总体布线应运而生
在现在的 VLSI设计中,随着制程技术的发展,纳米等级CMOS电路的电晶体密度剧烈增加,电路时延问题越突出,时序收敛越困难,最终严重影响芯片的性能和产量。当前,互连线延迟超越门延迟变成影响电路性能的主要因素,并且总体布线结果直接影响芯片面积、速度、可制造性、功率和完成设计周期所需的迭代次数,因此其在决定电路性能方面起着重要作用
较长的布线会导致明显的信号延迟并导致更大的动态功耗。**过多的通孔会降低芯片的可靠性。**电线间隔的差异会引起电短路或者断路而降低成品率。物理设计是人工设计中耗时最长和错误率最高的设计过程之一。它也是近年来电子设计自动化(Electronic Design Automation,EDA)工具中发展最快和自动化程度最高的领域之一。随着制造工艺的发展,它也是受到影响最大、面临的机遇和挑战最多的领域之一.
特征尺寸进入纳米级后,器件的尺寸变得越来越小,互连线的线宽越来越细、密度越来越大。互连线变小速度赶不上器件,长度也迅速增加,互连线的延迟远超过门的延迟,占到线网总延迟的 60%~70%。
集成度的增大使得互连线面积不断增加,约占芯片总面积的30%~40%。为了降低芯片大小,布线金属层的数量也在不断增加。目前最大布线层数已达到13层,预计 2028 年会达到 17 层。
为了缩短开发周期,IP复用显得越来越重要。这使得布线区域的障碍数量不断增多,密度增大,形状也更加复杂。此外,利用障碍内资源布线可大大缩短互连线长度、减小布线面积和提高芯片性能。当线网障碍内部分较大时,导致输出端的电压转换速率过大,引发噪音和功率问题,并影响信号完整性。这使得在布线过程中需要进一步考虑绕障问题和信号完整性问题
现代设计中互连结构和网格的高体积与复杂性对可布线性造成了严重的挑战。快速拥塞分析对于在设计的早期阶段解决可布线性问题变得至关重要,例如,在布局期与总体布线一起。在现代设计中,一些新的因素导致了布线拥塞,包括金属层之间明显不同的导线尺寸和间距、层间通孔的尺寸、各种形式的布线拥塞(例如,保留给电网、时钟线网或芯片系统中的JP块),由于引脚密度和总体单元内的布线导致的局部拥塞和位于较高金属层的虚拟引脚。然而,早期的评估技术都没有全面地捕捉到这些新的拥塞源。
布线问题已经被证明是一个 NP 完全问题,因此 ,为布线问题寻找全局最优解不具备可行性 另外 ,布线过程受制造⼯艺制约 ,存在着很多约束和限制 ,这也令布线的复杂度进一步提升
In advanced technology nodes, detailed routing has to deal with complicated design rules and large problem sizes, making its performance more sensitive to the order of nets to be routed.
迷宫布线(寻路算法) #
李氏算法(迷宫布线算法) #
该算法从源点开始 ,依次访问网格各⽅向上的相邻节点 ,并为该节点标记从源点到该点的已知布线代价。对每个访问到的节点重复相同的过程。这会在整个布线图中产生一个连续扩散的波 ,当这个波扩散到了目标点 ,即目标节点被他的相邻节点访问到时 ,就找到了这样一条路径连通源点与目标点。随后算法进入路径回溯阶段 ,从目标点开始 ,直到回溯到源点,此时就生成了一条最优路径
这类方法都是每次从线网(nets)中选择一条拆成两端线网来进行布线,效果取决于布线顺序。另外,算法未考虑约束(可布性、拥塞、间距),而这些约束都有滞后性,需要线网全部布线完成后,才能体现。因此基于以上方法的工作更多在顺序布线(sequential routing)前期就考虑各种约束[1-5]。
A*算法 #
(对李氏算法的改进,加速了李氏算法收敛)


- BFS
- Dijkstra
线搜索算法 #
Mikami 等在 1968年提出了第1个使用线段代替节点搜索的路径搜索算法–线搜索算法。该算法以源点和目标点为基点,首先从两个基点各引出两条相互垂直的直线,当直线遇到障碍物或布线区域边界时,会在当前的直线上选取新的基点并沿垂直方向生成一条新的直线,直到从源点和目标点延伸出的多级直线发生相交,则找到了一条路径连通源点和目标点。由于其并没有遍历所有的搜索空间,所以线搜索算法并不能保证找到最优解。 Hetze1在 2002年提出的Hetze1算法将以线段代替节点进行搜索的思想与A算法结合,在保证找到最优解的情况下具备比A算法更快的求解速度。
多源多汇迷宫布线 #
多源多汇迷宫布线将同一子树中的所有网格点视为源点,将另一个子树中的所有网格点视为汇点
并行算法 #
多商品流算法(multi commodity flow, MCF)
建模为整数线性规划(integer linear programming,ILP)
由商品的源点和目标点以及商品流经的路径组成。随后将整个布线区域建模成一个三维的布线网格,网格点可以作为商品流的流经点,点与邻近点之间的线段称作边。 在ILP 问题的模型中,网格的点和边作为变量用边和点的流量表示线网对边和点的使用情况,容量代表边和点上同时流经的最大的线网数量(在详细布线中一般取1)。目标函数为边上所有线网的流量与其相应布线代价的积的累加和。在约束条件下最小化目标函数可以获得布线的最短线长。其约束主要包含各个线网在点或边上的流量之和不超过点或边的容量约束、基于流量守恒定律的连通性约束等。
整数线性规划 #
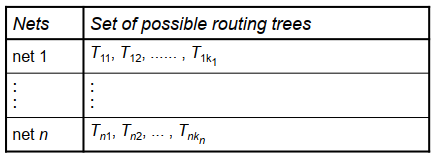
这类方法可以直接对所有线网布线(Concurrent Approach),并考虑交叉、拥塞等约束。算法提前生成端点之间可能的走线方案,并用一0-1变量 xij 表示是否选择本方案。问题随后转化为带约束的线性整数规划问题
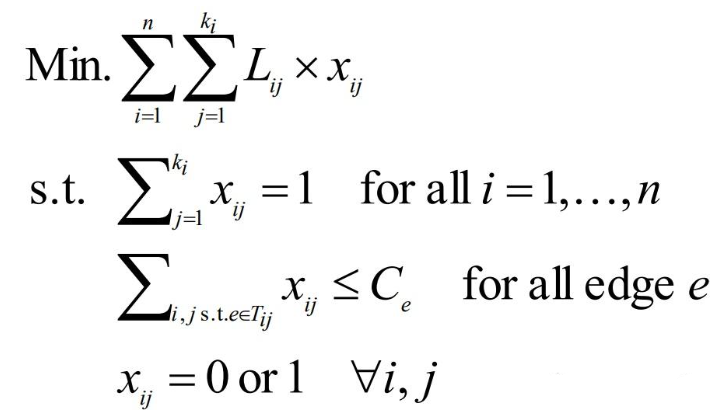
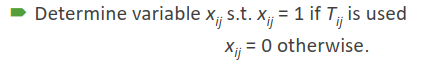
特点 #
Standard techniques to solve IP. No net ordering. Give global optimum. Can be extremely slow, especially for large problems. To make it faster, a fewer choices of routing trees for each net can be used. May make the problem infeasible or give a bad solution. Determining a good set of choices of routing trees is a hard problem by itself.
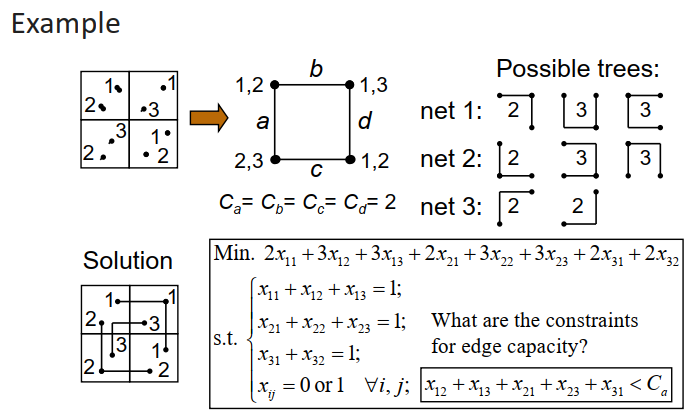
Hierarchical Approach #
Hierarchical Approach reduces global routing to routing problems on a 2x2 grid
先将网格划分为粗网格,找到粗网格间的布线,然后将网格细化,对每个子模块递归求解,每次求解规模均极小
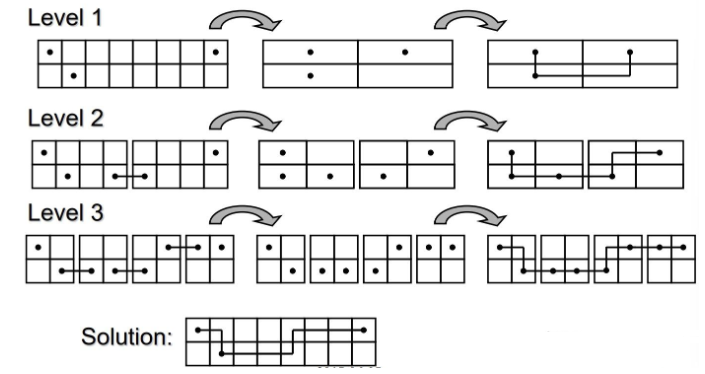
基于Steiner的算法 #
This technique can be used in global or detailed routing problems
对于某些多端net, 一般都采用最小斯坦纳(steiner)生成树方法。比如遵守水平垂直走线的Rectilinear Steiner Minimal Tree.一般生成树算法算法非常多,比如Kruskal,prime, spanning-graph[7],edge-substitution. 另外考虑实际布线中允许45,60度走线,也有对应八向斯坦纳最小生成树(octilinear steiner)方法[8].
定义 #
Steiner Node :
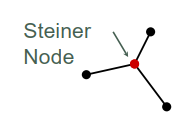
For a multi-pin net, we can construct a spanning tree to connect all the pins together
Steiner Tree: A tree connecting all pins and some additional nodes (Steiner nodes).
Grid graph:
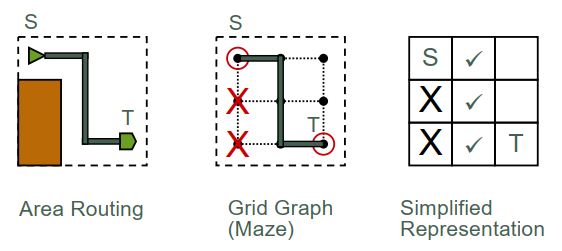
优化算法 #
布线从数学的角度来看是一个有约束的最优化问题。线网是指具有相同电位的一组引脚,很显然,这些引脚需要被连接在一起,但电路板上有着各种约束,代表性的便是一系列的匹配规则(比如对一部分版图设计初学者来说堪称莫名其妙的插指结构或重心匹配和热匹配),因此这是一个十分典型的复杂最优化问题。
优化指标 #
一般来说,最优化的主要指标是线长,但在RF设计中,线与器件的距离等其它因素将因为互感效应和一些非线性效应变得异常重要。VLSI总体布线问题最初以线长最小化为优化目标,但随着制造工艺的不断发展和芯片特征尺寸的不断缩小,互连线延迟对芯片性能的影响越来越大,因此,时延和串扰等优化目标也需要在总体布线问题中考虑。同时,影响到芯片的可布性和可制造性的因素,包括溢出数、拥挤度、通孔数等优化目标,也是当今总体布线工作需要优化的指标。
线长:线长影响了芯片的制造成本 ,且线长越长 ,线网的时延与电容越大 ,这会使芯片的稳定性下降、功耗增高
布通率:完成连线/实际连线数
通孔数量:越少越好,via具有更大延时,还会增加芯片制造失败率
串扰和时延:线网间的电容电感等现象会在线网间产生串扰 ,增大时延。因此布线算法要对时延敏感线网及关键线网做出特殊设计,以降低芯片的总时延,提高芯片稳定性
术语 #
(1)网表:N={N,N。,,…},其中每个线网N,是一个引线端的集合,属于同一个线网的引线端将由布线工具把它们连接在一起,这里的网表则是提供电路的互连信息。 (2)布线容量:指考虑设计规则、布线区域的大小和线网的宽度,布线区域内的最大走线数。 (3)拥挤度:需要的布线资源与可用的布线资源之间的比值。 (4)溢出边:若一条边的布线资源需求量大于可用的布线资源,则该边被称为溢出边。 (5)总体布线图(GRG):在进行总体布线之前,根据电路的几何特征和电路结构,用网格将整个芯片按行和列划分为若干称为总体布线单元的区域,并通过总体布线器指定GRC以连接线网。由网格线及其交点所构成的图的对偶图称为总体布线图。 (6)局部线网:若一个线网所需要连接的所有引脚均在同一个GRC中,则称该线网为局部线网。 (7)全局线网:若一个线网所需要连接的部分或全部引脚分布在不同GRC中,则称该线网为全局线网。 (8)设计规则约束:目前布线问题中存在一些基本设计规则约束(DesignRules Constraint,DRC)违反情况,包括开路、短路、相邻金属线的间距不足等。 (9)3D总体布线和2.5D总体布线:多层总体布线类型分为3D和 2.5D 总体布线两种。 ① 3D总体布线:对于多层布线,采用3D布线直接在立体的总体布线图进行布线,这样得到的总体布线方案虽然比2.5D来得更准确且能取得多个更好的性能指标,但会带来巨大的时间和空间复杂度。由于EDA设计的原则是简单、快速、合理,所以3D布线的研究不能令人十分满意。 ② 2.5D总体布线:是将多层布线中各层的布线资源、引脚等映射到平面上,将3D布线转化成平面布线,这样进行平面总体布线可减少时间空间复杂度,在平面上完成总体布线后,再通过层分配将布线结果还原到3D布线,同时维持平面布线获得的溢出数且优化通孔数。
标准 #
LEF #
Tools #
Glogal Router #
CUGR #
CUGR is a detailed routability-driven global router and its solution quality is solely determined by the final detailed routing results
Detail Router #
Tritonroute #
from openRoad
including pin access analysis, track assignment, initial detailed routing, search and repair, and a DRC engine.
当前研究方法 #
结合AI:比如使用AI模型预测拥塞率,在顺序布线早期阶段减少拥塞,降低时间。比如利用强化学习,自行学习走线过程。
布线-拆线:有点类似对抗生成网络**(GAN)**思想。Alpha-PD-Router有两个玩家,布线器(router)和拆线器(cleaner)。布线器以总线长为目标布线,而拆线器则拆线重布,以使布线器布线更容易为目标,如此往复下去。
相关竞赛 #
[ISPD24 Contest: GPU/ML-Enhanced Large Scale Global Routing | ISPD24_contest (liangrj2014.github.io)]( https://liangrj2014.github.io/ISPD24_contest/#:~:text=Global routing is a critical component)
[ISPD 2008 Global Routing Contest]( https://www.ispd.cc/contests/08/ispd08rc.html#:~:text=Continuing the tradition of spirited competition,)
[ISPD 2007 Global Routing Contest]( https://ispd.cc/contests/07/contest.html#:~:text=Continuing the tradition of spirited competition,)
[Initial Detailed Routing Contest at ISPD 2018]( https://www.ispd.cc/contests/18/#:~:text=This proposed contest focuses on the)
[Initial Detailed Routing Contest at ISPD 2019]( https://ispd.cc/contests/19/#:~:text=Detailed routing can be divided into)
- 评价标准
- Connectivity constraints
- LEF routing rules
- Routing preference metrics
- 评价标准
参考 #
大规模集成电路布线算法设计简介 - 知乎 (zhihu.com)
超大规模集成电路布线算法综述 (sciengine.com)
非曼哈顿结构下超大规模集成电路布线理论与算法-目录,第一章绪论